二叉树
- 树和节点的高度
- 树和节点的深度
完全二叉树
满二叉树
Perfect Binary Tree
二叉查找树
AVL树
自平衡二叉搜索树,在AVL树中任何节点的两个子树的高度最大差别为一,也就是说这种树会在添加或移除节点时尽量试着成为一棵完全树,所以它也被称为高度平衡树。查找、插入和删除在平均和最坏情况下都是 O(log n),增加和删除可能需要通过一次或多次树旋转来重新平衡这个树。 旋转分为L, R, LR, RL。
Treap 树堆
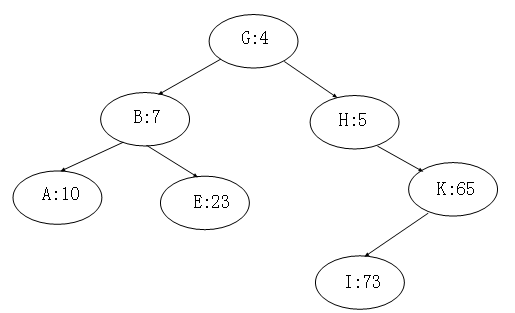
Treap每个节点记录两个数据,一个是键值,一个是随机附加的优先级,Treap在以关键码构成二叉排序树的同时,又以结点优先级形成最大堆和最小堆。所以Treap必须满足这两个性质,一是二叉排序树的性质,二是堆的性质。如下图,即为一个树堆。
树的遍历
不管是 DFS 还是 BFS,都是在出栈或出队时访问,入栈或入队保证的是访问的顺序。
深度优先遍历
借助堆栈实现
// node {
// val,
// left,
// right,
// visited, //
// pushed // 入栈或入队时打上标记,排除重复入栈/入队,这一点在树上不会出现,但在图中如果有环就会出现,或者在走迷宫时也会出现。
// }
// 先序遍历
function DepthFirstSearch(root) {
let stack = []
let nodeValues = []
if(root)
stack.push(root)
while(stack.length) {
let node = stack.pop()
if(node.right)
stack.push(node.right)
if(node.left)
stack.push(node.left)
nodeValues.push(node.val)
}
return nodeValues
}
function DFS(node) {
visit(node);
node.visited = true;
node.children.map(child => {
if(!child.visited)
DFS(child)
})
}
广度优先遍历
借助队列实现
function BreadthFirstSearch(root) {
let quequ = [],
nodeValues = []
if(root)
quequ.push(root)
while(quequ.length){
let node = quequ.shift()
if(node.left)
quequ.push(node.left)
if(node.right)
quequ.push(node.right)
nodeValues.push(node.val)
}
return nodeValues
}