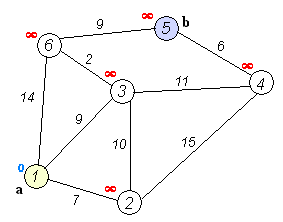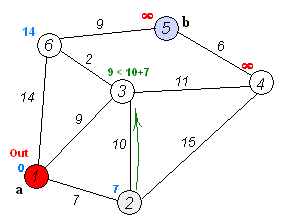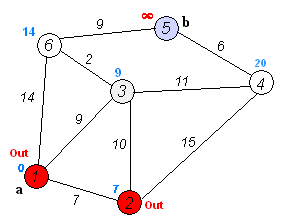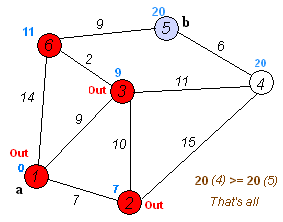
Dijkstra
单源最短路径算法,前提是无负权值边
// v0 是源点
// A[][] 是邻接矩阵
// dist[] 是 v0 到个点的最短距离
// path[] 是 v0 到 vi 的最短路径的前驱点编号
const int MAXINT = 32767;
const int MAXNUM = 10;
int dist[MAXNUM];
int prev[MAXNUM];
int A[MAXUNM][MAXNUM];
void Dijkstra(int v0)
{
bool S[MAXNUM]; // 判断是否已存入该点到S集合中
int n=MAXNUM;
for(int i=1; i<=n; ++i)
{
dist[i] = A[v0][i];
S[i] = false; // 初始都未用过该点
if(dist[i] == MAXINT)
prev[i] = -1;
else
prev[i] = v0;
}
dist[v0] = 0;
S[v0] = true;
for(int i=2; i<=n; i++)
{
int mindist = MAXINT;
int u = v0; // 找出当前未使用的点j的dist[j]最小值
for(int j=1; j<=n; ++j)
if((!S[j]) && dist[j]<mindist)
{
u = j; // u保存当前邻接点中距离最小的点的号码
mindist = dist[j];
}
S[u] = true;
for(int j=1; j<=n; j++)
if((!S[j]) && A[u][j]<MAXINT)
{
if(dist[u] + A[u][j] < dist[j]) // 在通过新加入的u点路径找到离v0点更短的路径
{
dist[j] = dist[u] + A[u][j]; // 更新dist
prev[j] = u; // 记录前驱顶点
}
}
}
}